Machine Learning Demystified

Are you new to Machine Learning? Are you wondering what all the buzz is about?

The purpose of this article is to acquaint you with the basic concepts and terminology of ML, and to prepare you to run your own ML experiments. 

My goal is to demystify Machine Learning.  While some ML algorithms may be complicated, the concepts are surprisingly easy to grasp, and the tools are easy to use for anyone with basic programming skills.  This article should provide you enough knowledge to get the neuron’s popping with ideas as to how you might use ML in your work or life.  My next article “Using HPCC Machine Learning” will provide a tutorial on utilizing the HPCC Machine Learning Bundles.

If you prefer video learning, here is a presentation I gave to the HPCC Community Day participants in Atlanta last fall.  In 15 minutes it covers the contents of this article, plus a tongue-in-cheek allegory to cement the concepts in your mind using a (rather feeble) attempt at humor.

Machine Learning Basics

Machine Learning covers a fairly wide range of activities, and there are several distinct types of ML.  You may have heard the terms: supervised-learning, unsupervised-learning, reinforcement-learning, deep-learning, et cetera.  The predominant applications of machine-learning today, however, utilize “supervised-learning”, and this is the topic I will discuss today.

Throughout this article, when I refer to Machine Learning, I am specifically referring to the “supervised” form of ML.

The basic premise of supervised ML is as follows:

The data-samples are known as the “Independent Variables” because they are the given information and are not dependent on any other data.  The Independent Variables are also known as the “Features” of the data.

The target values are known as “Dependent Variables” because they are (hopefully) in some way dependent on the data-samples.

The Independents and Dependents together are known as the “Training Set”.

Now the ML algorithm’s job is to determine how to map Independents to Dependents.  Each ML algorithm has a different set of tricks for making this mapping.

The mapping function which the ML algorithm produces is called a “Model”.  Each model represents a “Hypothesis” about the relationship between the independent variables and the dependent variables.

It may be a good hypothesis, or a bad hypothesis, but regardless, the model represents a single hypothesis.

The hallmark of Machine Learning is the ability to “generalize” about the relationship.  It’s not enough to say: “If you see a, then the answer is b”.  That is simply recall.  Machine learning aims to predict a reasonable answer when presented with data which it has never seen before.

Machine Learning Example Problem

Starting to make sense?  Here’s a simple example:

    Given the following data about trees in a forest (our Training Set):

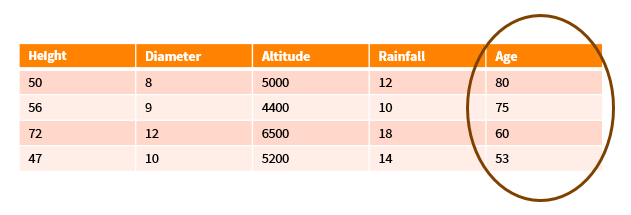
• We want to learn how to calculate a tree’s age (Dependent Variable) from data about the tree’s Height, Diameter, Altitude, and Rainfall (Independent Data).
• If you look at the data, it’s hard to see how you would combine the independent variables in any fashion to predict the tree’s age.  This is what ML algorithms are good at.  They can find subtle signals in the input (i.e. Independent) data that can be mapped to an output (Dependent) variable.
• Machine Learning will automatically construct a model that attempts to  minimize some sort of  “prediction error”.
• In addition, the ML Model (depending on the algorithm) may provide insights into the discovered relationships.  We’ll come back to this.

Note that there is no inherent directionality in the training set above.  We could instead have asked ML to learn to map Height, Altitude, Rainfall and Age to the tree’s Diameter.  It might be silly to do that however, since it would require us to measure the trees age (e.g., cut it down and count the rings) in order to determine the diameter, which we could have easily obtained with a tape measure.  Typically, with ML, we want to map easy-to-measure variables (known as “observed” variables) to difficult to measure (i.e. “unobserved”) variables.

Quantitative and Qualitative Problems

Supervised Machine Learning supports two major types of problem:

• Qualitative – e.g., Determine the species of the tree / Determine if the tree is healthy or not.
• Quantitative – e.g., Determine the numerical age of a tree

Learning a Qualitative model is called “Classification”.

Learning a Quantitative model is called “Regression”.

Don’t try to make sense of the term “Regression”.  It is an archaic term that has only an obscure relationship to its meaning.  When you hear regression, think “predict a numeric value”.  “Classification”, on the other hand is intuitive.  I’m trying to classify the tree as healthy / unhealthy, or as “Maple”, “Spruce”, “Cedar”, etc.

Types of Model

There are dozens of different ML algorithms that all serve the same purpose: Classification and/or Regression. These algorithms differ in the types of Model (Hypothesis) that they can produce, as well in the way that they choose the “best hypothesis”.  The space of all the hypotheses that a given algorithm can produce is known as its “Hypothesis Set”.  The way that it chooses the best hypothesis out of its set is known as the “learning algorithm”.

There are various classes of ML algorithm that share similar hypothesis sets.  These include:

• Linear models assume that the dependent variable is a function of the independent variables multiplied by a coefficient (e.g. f(field1 * coef1 + field2 * coef2 + … + fieldM * coefM + constant))
• Tree models assume that the dependent variable can be determined by asking a hierarchical set of questions about the independent data.  (e.g. is height >= 50 feet? If so, is rainfall >= 11 inches?…then age is 65).
• Other models such as Neural Network models don’t have an intuitive interpretation (except mathematically).  As such, they are not considered “Explanatory” models, though they may do a fine job of prediction.

Depending on the application, it may be important to use “Explanatory” models, that provide visibility into the decision process (i.e. the hypothesis).  This is the case where the goals of the ML include “insight” about data and its relationships.  It is also important when there is a need to justify the inferences incorporated in the model (for example to regulators) or whenever “because it works” is not a good enough answer.

Conclusion

Machine Learning is Fun and Easy 

You now know enough to be dangerous.  Think about all the things you can predict and all the insights you can gain from your data.  Feel free to experiment.  ML tools are simple to use and can provide you with hours of fun and allow you to test all sorts of interesting ideas.  My next article: “Using HPCC Machine Learning” will show you how to utilize the HPCC ML Bundles to do so.

But…

But I have to sound this obligatory warning:

ML’s conceptual simplicity is somewhat misleading.  Each algorithm has its own quirks — assumptions and constraints — that need to be taken into account in order to maximize the predictive accuracy.  Furthermore, quantifying the efficacy of the predictions require skills in data-science and statistics that most of us do not possess.  For these reasons, it is very important that we do not use our exploration of ML to produce products or make claims on abilities without first consulting experts in the field.

Here are a few of the potential pitfalls of Machine Learning:

• Overfitting — Many algorithms tend to overfit the training set.  That means that it is reducing the prediction error by fitting to the noise that happens to be in that set of data.  An overfit model will treat that noise as signal, and use what it learned to predict the next data you present.  Unfortunately that next set of data will have been subject to a completely different set of noise, which will not give good results.  There are techniques for resisting overfitting — some implemented within the algorithms, and some requiring calibration (“regularization”) or other tricks.
• Data Problems — It is rare to find a perfect dataset that contains no errors, has no missing values, and is consistent in every aspect.  There are data-scrubbing techniques which must be done in order to obtain optimal results with ML.
• Mismatched Assumptions — Using a linear model to represent an exponential relationship will not yield good results.  This may require the data to be transformed (e.g. by applying a log scaling to certain variables) or taking the log or exponent of the results.  Some algorithms assume that the errors in your data follow a certain probability distribution (e.g. Normal / Binomial).  If that is not true of your data, that your data may not be compatible with that particular algorithm.
• Inadequate Training Data — For some problems, 100 data points might be plenty to learn accurate prediction.  For other problems, a hundred thousand data points might be insufficient.  It is tied to the complexity of the space being modeled, which is determined by many factors such as: number of features, cardinality (how many values?) of the features, complexity of the underlying relationships, and the cardinality of the result.  Another common problem is when the training set is not representative of the population for which you are trying to predict.  A training set containing only good transactions cannot help you identify bad transactions.
• Improper Assessment — There a numerous ways to make mistakes in assessing the effectiveness of the resulting model.  One way is to test your model on the same data that you trained it with.  This will give accuracy statistics that are literally unbelievable!  Another is to try every different algorithm and pick the one that does best on your test data.  You’ve just inadvertently fit your model to a particular test sample, and biased the expected accuracy accordingly.
• Feature Relevance — You can’t predict tomorrows stock market close based on today’s temperature.  You may get a model that does a good job of fitting the training set, but no matter how big your training set is, it will have poor results on data outside of that set.

Now don’t let that get you down.  Have fun.  Let those neurons fire.  Experiment away!  As long as you don’t stake your reputation on the results of your unverified experiments, what’s the worst that can happen?