Fast Edit Distance Queries for Big Data Using Prefix Trees
In this blog post, I will walk you through using prefix trees and a big-data platform to build fast edit-distance queries. You can use the examples here to begin processing large volumes of data using an edit-distance algorithm or to build queries fast enough to query very large datasets interactively using an edit-distance algorithm. This blog post builds on a previous blog post. Please read my last blog post here to understand why the approach below works and to understand my method to rapidly build prefix trees for big data.
In order for us to query a prefix tree, we need to think about our query in two ways. First, we need to set up our query so that as we feed it nodes from the prefix tree, we can continue to bring the current state forward. This is pretty easy to do with a good record structure and a recursive JOIN operation. You’ll see this later. Our second task focuses on how to use an edit distance algorithm with the prefix tree. We need to adjust our edit distance algorithm so that it is iterative. This is so we can feed it nodes from the prefix tree and evaluate branches in the tree as we go along.
Feeding an Edit Distance Algorithm
Edit distance algorithms generally compare two words at a time and usually model those two words using a 2-dimensional matrix. A matrix is built for each word pair in question. Below is one such matrix for the words “cats” and “caps”.
| c | a | p | s | ||
| 0 | 1 | 2 | 3 | 4 | |
| c | 1 | 0 | 1 | 2 | 3 |
| a | 2 | 1 | 0 | 1 | 2 |
| t | 3 | 2 | 1 | 1 | 2 |
| s | 4 | 3 | 2 | 2 | 1 |
The answer, meaning the edit distance, is the number in the lower right hand corner of the matrix. For cats and caps, the answer is 1. This means that a single edit is required to turn caps into cats or cats into caps.
How we build the matrix is not important for this discussion (there are many algorithms to choose from). What is important is that we need to modify our edit distance algorithm to an iterative approach. We need to be able to take the last known state and pass that state into an edit distance function along with the next node in our prefix tree.
Below is an edit distance function I modified for our purpose. It is modified to be used as an in-line C++ function. It is also modified so that it is an iterative edit distance function that returns state back to our ECL program.
STRING CalculateLevenshteinVector(STRING word, STRING node, STRING state) := BEGINC++
/// CFK 08/20/2015 charles.kaminski@lexisnexis.com
/// This C++ returns the vector used to calculate
/// the Levenshtein distance in an interative process so that
/// an efficient trie structure can be traversed when finding candidates
/// Node values can be passed in and the current state can be saved
/// in the return vector so that other nodes can be further processed in series
/// We're using char arrays to keep the size down
/// That also means that all our words (both in the trie and our query words)
/// must be less than 255 characters in length. If that limitation becomes a problem
/// we can easily use an array of integers or another other structure to store
/// intermediate values.
#option pure
#include
#body
// The last element in the array will hold
// the min value. The min value will be used later.
int v_size = lenWord + 2;
unsigned char min_value = 255;
unsigned char new_value = 0;
// Since v0 is not returned, we should not use rtlMalloc
//unsigned char * v0 = (unsigned char*)rtlMalloc(v_size);
unsigned char v0[v_size];
// We use rtlMalloc helper function when a variable is returned by the function
unsigned char * v1 = (unsigned char*)rtlMalloc(v_size);
if (lenState < 1){
for (int i = 0; i < v_size; i++){
v0[i] = i;
}
}
else{
memcpy(&v0[0], &state[0], v_size);
}
int cost = 0;
int k = v0[0];
for (int i=k; i<k+lenNode; i++)
{
min_value = 255;
v1[0] = i + 1;
for (int j=0; j<lenWord; j++)
{
cost = (node[i-k] == word[j]) ? 0 : 1;
new_value = std::min(v1[j] + 1, std::min(v0[j+1] + 1, v0[j] + cost));
v1[j+1] = new_value;
if (new_value < min_value){
min_value=new_value;
}
}
memcpy(&v0[0], &v1[0], lenState);
}
// Store the min_value;
v1[v_size-1] = min_value;
__lenResult = v_size;
__result = (char *) v1;
ENDC++;
Now you have an edit distance function that saves state, but there’s an additional critical task we need to perform with our edit distance algorithm. We need to know, given the current state, what the minimum edit distance will be for the current branch of the prefix tree. Stated in another way, there is a minimum edit distance that can be derived from the current state. This means that regardless of what we pass into the function in the future, all child nodes will have an edit distance greater than or equal to that current minimum edit distance.
We need to know this number because if the minimum distance for a branch is greater than the maximum distance we are going to allow, we want to prune this branch of the prefix tree. It doesn’t make sense to move forward with a branch of the tree if we know that any future nodes on the tree will have an edit distance greater than the maximum distance we are willing to accept. There are real cost savings in pruning a branch.
If you take a closer look at the function above, you will see a minimum value being calculated in the loop and stored in the final state returned. The second function below allows us to find that minimum value. Also included is a third function below that returns the final edit distance.
UNSIGNED1 GetMinDistance(STRING state) := BEGINC++ /// CFK 08/20/2015 charles.kaminski@lexisnexis.com /// Get the Minimum Edit Distance #option pure #body //return (unsigned char) state[(unsigned int) position]; return (unsigned char) state[lenState-1]; ENDC++;
UNSIGNED1 GetFinalDistance(STRING state) := BEGINC++ /// CFK 08/20/2015 charles.kaminski@lexisnexis.com /// Get the Final Edit Distance #option pure #body //return (unsigned char) state[(unsigned int) position]; return (unsigned char) state[lenState-2]; ENDC++;
Putting It All Together
So now we have a workable edit distance function that can interface with our prefix tree and we have the ability to identify when we need to prune a branch in the prefix tree using the minimum edit distance for a branch. We glue these pieces together using the JOIN attribute. In the example far below, I use JOIN to walk each level of our tree while pruning branches as I go, but we’re not there yet.
You can walk each level of the prefix tree with multiple recursive JOINs, but you won’t know how many times to run the JOIN. That’s where LOOP comes in. I use LOOP to run JOINs recursively, to control when records (nodes and branches) are pruned, and to signal when to end the LOOP. The LOOP ends when we run out of additional child records to process because there are no more levels in the branches that haven’t been pruned.
So now the pieces are conceptually glued together with JOIN and LOOP, but we still need a few more bits before I show you the JOIN and the LOOP in action. You need a query dataset. You also need a TRANSFORM to hold logic and call functions from within the JOIN. For the query dataset, you can take the original input dataset from my last blog post on creating prefix trees and use it to query the prefix tree. In order to do this, the input dataset needs to be converted into the layout used inside LOOP. The code below converts the input dataset into the layout we need.
QueryPTLayout := RECORD
input_ds;
STRING state := '';
DATA state_data := (DATA)'ab';
UNSIGNED node_id := 0;
STRING node := '';
BOOLEAN is_word := False;
STRING cumulative_nodes := '';
UNSIGNED1 cumulative_node_size := 0;
UNSIGNED1 current_distance := 0;
UNSIGNED1 final_distance := 0;
END;
query_ds := PROJECT(input_ds, QueryPTLayout);
output(query_ds, named('Query_DS'));
Now we need a transform we can use from within the recursive JOIN. Notice that the transform takes the previous state data and runs it through our edit distance function along with additional node-data from our prefix tree.
QueryPTLayout QueryPTTransform(QueryPTLayout L, PTLayout R) := TRANSFORM
SELF.word := L.word;
SELF.state := IF(R.is_word, L.state,
CalculateLevenshteinVector(L.word, R.node, L.state));
// The state data reformatted for easier debugging
SELF.state_data := (DATA)SELF.state;
// The current node ID of the prefix tree.
// This will be joined against parent id to find the next node
SELF.node_id := R.id;
// The text of the node
SELF.node := R.node;
// If true, this is an end-cap word in the tree and has no children
SELF.is_word := R.is_word;
SELF.cumulative_node_size := IF(R.is_word, LENGTH(R.node),
LENGTH(R.node) + L.cumulative_node_size);
// The node and it's parent values put together
SELF.cumulative_nodes := IF(R.is_word, R.node, L.cumulative_nodes + R.node);
SELF.current_distance := IF(R.is_word, L.current_distance, GetMinDistance(SELF.state));
SELF.final_distance := IF(R.is_word, GetFinalDistance(SELF.state), L.final_distance);
END;
Finally, we have all the bits and pieces to build a recursive JOIN wrapped in a LOOP. The JOIN walks through our prefix-tree levels using the id and parent-id relationship in the prefix-tree nodes. This happens while the LOOP also prunes branches of our prefix tree along the way.
MAX_DISTANCE := 2;
looped_ds := LOOP(query_ds,
LEFT.is_word = False,
EXISTS(ROWS(LEFT)) = True,
JOIN(ROWS(LEFT), final_pt_ds,
LEFT.node_id = RIGHT.parent_id and
LEFT.current_distance < MAX_DISTANCE,
QueryPTTransform(LEFT,RIGHT), INNER));
OUTPUT(looped_ds(looped_ds.final_distance < MAX_DISTANCE), NAMED('Final'));
Performance, Additional Testing, and Code Examples
I’ve written three forms of this code. You can download them here.
The first form is self-contained and runs on a Thor using the in-line dataset in the example. Use this one to understand what is going on with prefix trees and how to query them in Thor using an edit-distance algorithm.
The second form is mostly the same, but I’ve written it to take a data file from a Thor, build the prefix tree and then use the same data file to query the prefix tree. You will need to edit this code for your own data file. I tested this on a 1.7 million-record dataset with a 21-node Thor using slower spindle storage drives. The prefix tree builds in about 5 seconds. The 1.7 million-record dataset is used again to walk the prefix tree in about 45 minutes. That’s the equivalent of taking two 1.7 million-record datasets and finding all edit-distance candidates between them (think Cartesian join) in 45 minutes. The naive approach would have to churn through almost 3 trillion candidate pairs. This approach is orders of magnitude faster. You can easily edit this example to use different datasets to build and separately query your prefix tree.
The final form of the code is similar to the other two examples, but I broke the code out into an example Thor job and Roxie query. Like the second form above, you will need to edit this code for your own data file. The Thor job builds the prefix-tree. The Roxie query queries the prefix tree interactively and reports back performance data. Also included is a very simple python script I wrote to query the prefix tree and collect performance data. I ran a thousand queries on three separate runs using a single-node Roxie with spindle disk drives. On the final run, the average performance time was 24.7 milliseconds. The standard deviation for the run was 7.2 milliseconds. You can see the performance graph below.
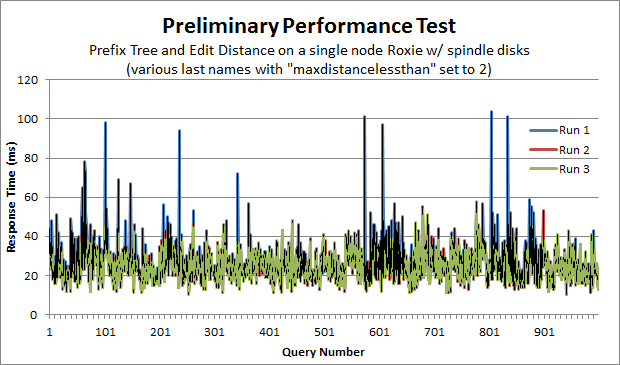
Finally, if you’ve found the blog posts or the code useful, please say so in the comments section after logging in, through GitHub, or drop me a line.
-Charles
###Update###
Submitted by ckaminski on Sat, 01/07/2017 – 4:16pm
I’ve created a set of function macros that can do the heavy lifting for you. Check them out at https://github.com/Charles-Kaminski/PrefixTree
-Charles
