Automatically Cluster your Data with Massively Scalable K-Means

Imagine you are sitting in front of thousands of articles and trying to organize them into different folders. How would you accomplish it and how long would you expect to finish it? Reading all the articles one by one and spending days or even months to finish the task? If you have some sort of data but have no clue how to efficiently cluster them, then this article should be a right place to start.

In this article,  KMeans bundle, an efficient tool to automatically cluster unlabeled data will be introduced. It is an implementation of K-Means algorithm, an unsupervised machine learning algorithm to automatically cluster Big Data into different groups.

The implementation of  K-Means algorithm in HPCC Systems adopts a hybrid parallelism to enable K-Means calculations on massive datasets and also with a large count of hyper-parameters. The hybrid parallelism can be realized by utilizing the flexible data distribution control and Myriad Interface of HPCC Systems.  Further more, the article also includes the details of how to apply KMeans bunle to cluster your data step by step.

If you are new to machine learning or interested in supervised learning, the blog Machine Learning Demystified is a great resource. It reviews the basic concepts, terminology of Machine Learning and how to utilize supervised machine learning.If you are interested in the details of Myriad Interface, you may want to start from this article. This article also assumes that you have at least some basic ECL programming skills, which you can get by reading our ECL documentation or  taking an online training course by clicking here.

Unsupervised Learning and K-Means Clustering Algorithm

Machine learning algorithms can be roughly categorized into two types based on their requirement for training data: supervised learning and unsupervised learning. Unsupervised learning is comprised of machine learning algorithms that do not require labeled training data. Within the unsupervised category, K-Means is by far the most popular clustering algorithm and is extensively used in scientific and industrial applications. K-Means has been widely used in many different fields, including education, agriculture, fraud detection, public transportation, IoT management.

K-Means groups an unlabeled dataset of P observations into a predefined K number of clusters, so that the resulting clusters have high intra-cluster similarity. If centroids are m_1, m_2, … m_k,  partitions are c_1, c_2, … c_k and cluster members are  x_1, x_2,…x_p,  then one can attempt to minimize the objective distance of K-Means  as:

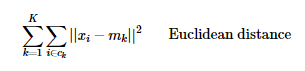
To initiate the clustering process, the K-Means algorithm takes the number of clusters K and the initial position of the centroids (the center of each cluster) as model parameters. After initialization, the K-Means model starts an iterative process which keeps updating the position of the centroids and their associations with the observations. There are two major steps in the iterative process: assignment step and update step.

With a set of k centroids, the assignment steps first calculate the distances from each observation to each centroid via Euclidean distance. All observations p are assigned to their nearest centroid. The observations assigned to the same centroids are regarded as a cluster S_i at iteration t. The assignment step can be described mathematically as below: 

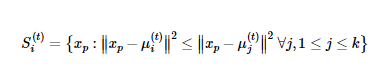
The next step is the update step. The centroids are updated or repositioned by calculating the new mean of the assigned observations, which is the mean of the least squared Euclidean distance. As described mathematically in below equation, we update the new position of each centroid by summing up the samples in each cluster and divided by the number of members to get the new mean for iteration t + 1.

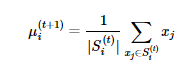
The final position of the centers are generated and the iterations stop when all observations remain at the assigned centroids and therefore the centroids would not be updated anymore. In practice, a maximum number of iterations and a converge rate or tolerance are defined to avoid an indefinite number of iterations and unnecessary computations. In this case, the K-Means algorithm will stop iterating once it reaches the maximum number of iterations or the movement distance of each center is smaller than the tolerance. 

Using K-Means Bundle in HPCC Systems

This section uses the well-known flower dataset Iris as an example to introduce how to apply K-Means bundle to cluster the real data step by step.

Step 1:  Installation

1. Be sure HPCC Systems Clienttools is installed on your system.

2. Install HPCC Systems ML_Core
   From your clienttools/bin directory run: 

   ecl bundle install https://github.com/hpcc-systems/ML_Core.git

3. Install HPCC Systems PBblas
   From your clienttools/bin directory run: 

   ecl bundle install https://github.com/hpcc-systems/PBblas.git

4. Install the HPCC Systems KMeans bundle. Run:

   ecl bundle install https://github.com/hpcc-systems/KMeans.git

Note that for PC users, ecl bundle install must be run as Admin.  Right click on the command icon and select “Run as administrator” when you start your command window.

Step 2: Import Machine Learning Bundle

Before starting running machine learning models, we have first to IMORT them into our environment as below:

IMPORT KMeans;
IMPORT ML_Core;

Step 3: Import Raw Data

The flower dataset Iris comes with the KMeans bundle. To import the data, simply type in below ECL code:

//Import raw data.
Raw_data := KMeans.Test.Datasets.DSIris.ds;

Step 4: Put Raw Data into Machine Learning Dataframe

In HPCC System, machine learning datasets are held in the dataframes defined in ML_Core bundle including NumericField dataframe and DiscreteField dataframe, etc. To put our data in NumericField dataframe, you can type in below source code:

//Hold the raw data in machine learning dataframes such as NumericField
// Add id to each record
ML_Core.AppendSeqId(raw_data, id, Raw_with_id);
// Transform the records to NumericField dataframe
ML_Core.ToField(Raw_with_id, ML_data);

Note: This creates the ML_data attribute containing the data

For more information on the ToField Macro, see Using HPCC Systems Machine Learning

Step 5: Initialization

Let’s start to define the initial centroids

//Initialization
Centroids := ML_data(id IN [1, 51, 101]);

Step 6:  Run K-Means model

To run K-Means model, as introduced in the above section, in reality it needs a pre-defined tolerance and maximum iterations. Here we define them as blew:

//Setup model parameters
Max_iterations := 30;
Tolerance := 0.03;

Then we can fit the model with our data as following:

//Train K-Means Model
//Setup the model
Pre_Model := KMeans.KMeans(Max_iterations, Tolerance);
//Train the model
Model := Pre_Model.Fit( ML_Data(number < 5), Centroids(number < 5));

Note: Here we filter out the unnecessary attributes out via filter (number < 5).

After the model is built, we can take a look where the final position of the centroids using the Centers function:

//Coordinates of cluster centers
Centers := KMeans.KMeans().Centers(Model);

Step 7: Predict the cluster index of samples.

If you have some new samples and would like to know which clusters they belong to, you can predict it with the model we just built. In this case, we can use the predict function as following:

//Predict the cluster index of the new samples
Labels := KMeans.KMeans().Predict(Model, NewSamples);

Conclusion

As a simple but all-around unsupervised algorithm, the K-Means algorithm is the most well-known and commonly used clustering algorithms and has been widely utilized in various fields.  This article introduce the detail of the massively scalable parallel K-Means algorithm to handle Big Data on the HPCC Systems platform and how to apply it to your data step by step.  Welcome to the Big Data clustering world leveraging the distributed computing environment of HPCC Systems.

Find out more…

1. For more details, please see our paper.
2. Read Roger’s introductory blog which focuses on Demystifying Machine Learning.
3. Find out about Using PBblas on HPCC Systems
4. We have restructured the HPCC Systems Machine Learning Library. Find out more about this and future improvements.